La Macchina di Turing: descrizione generale
E veniamo a questo benedetto calcolatore ideato da Turing
negli anni trenta, che tanto ha fatto parlare il mondo di
allora, come quello di oggi. Innanzitutto, la macchina di
Turing (per brevità d'ora in poi la indicheremo anche col
suo acronimo MDT) non è fisicamente realizzabile per il
solito motivo della memoria illimitata. Essa quindi non va
intesa come una vera e propria macchina ma come un modello
matematico
 di un oggetto capace di calcolare. Se
però
dimentichiamo per un attimo la memoria, la MDT diventa un
oggetto, non solo tangibile, ma realizzabile con pezzi
elettromeccanici di fortuna come dei ricambi di un
registratore a bobina e una manciata di componenti allo
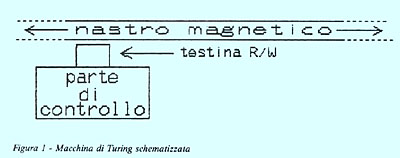
stato solido di vario genere. Infatti, una MDT è composta
essenzialmente da tre parti: un nastro magnetico, una
testina di registrazione/riproduzione e una parte di
controllo (figura 1).
di un oggetto capace di calcolare. Se
però
dimentichiamo per un attimo la memoria, la MDT diventa un
oggetto, non solo tangibile, ma realizzabile con pezzi
elettromeccanici di fortuna come dei ricambi di un
registratore a bobina e una manciata di componenti allo
stato solido di vario genere. Infatti, una MDT è composta
essenzialmente da tre parti: un nastro magnetico, una
testina di registrazione/riproduzione e una parte di
controllo (figura 1).
Il nastro, suddiviso in celle ed usato come memoria di
lettura e scrittura, ha lunghezza illimitata e viene
utilizzato sia per leggere i dati in ingresso (qualcuno
provvederà a inciderlo, prima di fare partire il tutto),
sia per i calcoli intermedi, sia per i scrivere i risultati
prima di terminare l'elaborazione.
Per definizione di MDT, il nastro prima di una computazione
è interamente blank tranne un insieme finito (volendo,
anche illimitato, ma non infinito) di celle. In queste, come
già detto, sono incisi i dati del programma.
La testina di lettura-scrittura, come è facile prevedere,
legge e scrive sulle celle del nastro magnetico che, proprio
sullo stile di un registratore, scorre davanti a questa.
Infine, la parte di controllo, serve per elaborare quanto è
inciso sul nastro dando ordini sia alla testina che al
meccanismo di scorrimento del nastro.
A questo punto dovrebbe essere ben chiara la semplicità di
tutto l'apparato: ripetiamo, l'unico problema è il nastro
illimitato, se no l'avrebbero realizzata. Anche perché a
tutt'oggi non è stato ancora trovato un formalismo capace
di calcolare più cose della MDT: equipotenti sì, ma più
potenti no.
Giusto per chiarire subito una cosa, vogliamo aggiungere che
anche un VIC-20 con memoria infinita sarebbe equipotente
alla MDT: di questa se ne parla con tanta ammirazione
proprio per la sua semplicità e per il fatto di essere
stata ideata e studiata negli anni trenta.
Il funzionamento
Detto questo, vediamo come funziona una MDT. Innanzitutto
una cella del nastro può contenere o il carattere blank
oppure uno dei caratteri del cosiddetto alfabeto del nastro:
in genere una manciata di simboli qualsiasi (in numero
finito), di solito quelli che conviene a noi trattare, come
le cifre binarie 0 e 1, le cifre decimali, le lettere
dell'alfabeto inglese o altro.
La parte di controllo, ha al suo interno il programma da
elaborare e funziona a stati finiti: ovvero durante
l'elaborazione, a seconda dello stato del calcolo, assumerà
un proprio stato interno. Operativamente parlando, la parte
di controllo legge dal nastro un simbolo, a seconda di
questo e del suo stato interno deciderà (univocamente):
a) cosa riscrivere sul nastro nella medesima cella
b) se posizionare la testina sulla cella a destra o a
sinistra della cella appena letta
c) in quale dei suoi possibili stati interni
traslare.
Univocamente nel senso che se dovesse ritrovarsi in un
secondo momento nelle stesse condizioni (stesso simbolo in
lettura e stesso stato interno) effettuerà come conseguenza
le stesse operazioni di prima.
Riassumendo il tutto, abbiamo che una elaborazione completa
corrisponde a preincidere il nastro con i dati del
programma, a memorizzare questo nella parte controllo e, a
elaborazione ultimata, leggere dal nastro stesso il
risultato del calcolo.
Il programma
Il programma della parte controllo altro non è che una
bella tabellina che riassume ciò che questa dovrà fare in
funzione del suo stato interno e del simbolo in lettura. La
suddetta tabella conterrà quindi un insieme di quintuple
del tipo (q,s,q',s',{D|S}) che identifica una precisa
transizione della macchina di Turing. "q" è lo stato
interno della parte controllo, "s" il simbolo appena letto
dal nastro, "q'" il nuovo stato interno dopo tale lettura,
"s'" il nuovo simbolo inciso sul nastro, nella stessa cella
dove è avvenuta la lettura. {D|S} sta a indicare che la
quinta posizione della quintupla è occupata da una D o da
una S ovvero dove la testina dovrà spostarsi dopo la
lettura e scrittura: a sinistra o a destra. Si noti che
tanto il nuovo simbolo quanto il nuovo stato non
necessariamente sono diversi da quelli precedenti.
Detto ciò se ad un certo istante la machina di Turing si
trova nello stato qi e legge dal nastro il simbolo si,
non fa altro che andare a cercare tra le sue quintuple
quella che inizia per (qi,si) e comportarsi di
conseguenza. Se tale quintupla non c'è, vuol dire che il
calcolo è terminato e la MDT può arrestarsi.
Ad esempio: con stato interno q0 e simbolo in lettura "1",
se nella nostra tabella abbiamo la quintupla (q0,1,q1,b,S)
significa che dobbiamo scrivere un blank, spostarci a
sinistra e passare nello stato interno q1... con stato
interno q2, simbolo in lettura blank e quintupla
(q2,b,q2,b,D) rimarremo nello stesso stato, riscrivendo il
simbolo blank per poi spostarci a destra.
Essendo il calcolo deterministico, come detto, non possono
esistere due quintuple con uguale stato e simbolo in lettura
e parte rimanente diversa, che indurrebbero un comportamento
non deterministico della macchina: aleatoriamente dovrebbe
scegliere tra due comportamenti diversi. Ciò induce una
rappresentazione più compatta e leggibile delle quintuple
di una macchina di Turing: una tabella bidimensionale che ha
per ascissa il simbolo in lettura e per ordinata lo stato
interno le cui caselle contengono la tripla rimanente. A
questo punto leggere cosa fare col dato simbolo e stato
interno non vuol dire altro che (stile battaglia navale) far
incrociare le due coordinate e leggere nella casella così
trovata.
Sembra evidente a questo punto che senza un po' di esempi si
rischia fortemente di diventare scemi.
Qualche esempio
Vedremo ora alcune macchina di Turing, programmate per fare
delle semplici operazioni. Vista la non limitatezza della
stessa, applicazioni più complesse richiedono solo insiemi
di stati più grandi e relativa tabella delle transizioni
opportunamente dimensionata: per ragioni di spazio ci
occuperemo solo di casi semplici.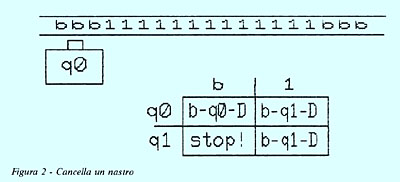
Un primo esempio, potrebbe essere una macchina di Turing che
preso un nastro su cui sono incisi un certo numero di "1"
contigui restituisce un nastro completamente blank. La
situazione è mostrata in figura 2: dato che gli "1" possono
essere solo in numero finito, è facile immaginare il nastro
tutto blank fino a un certo punto, poi una quantità più o
meno grande di "1" e dopo questi di nuovo tutti blank. Nella
configurazione iniziale, la macchina è posizionata sui blank iniziali (a sinistra, per esempio) e il suo compito
possiamo suddividerlo in due fasi: dapprima scorrere il
nastro verso destra finché non troviamo un "1" e,
trovatolo, cambiare questo e i successivi con um blank
finché non finiscono. Senza accorgercene abbiamo già
identificato i due stati interni della macchina: ricerca e
sostituzione che indicheremo rispettivamente con q0 e q1.
Sempre in figura 2 è mostrata la tabella relativa al
programma di cancellamento nastro e, indicato nella parte
controllo della MDT, lo stato iniziale col quale viene
avviata la macchina.
Uno sguardo alla tabella per rendersi subito conto della
semplicità di una di queste macchine. In ogni posizione
della tabella, identificata come detto da una ascissa
(simbolo in lettura, b sta per blank) e da una ordinata
(stato del controllo), leggiamo cosa la macchina farà in
ognuna delle possibili situazioni. Ad esempio, con stato
interno q0 e simbolo in lettura blank leggiamo nella
corrispondente casella la scritta b-q0-D: significa che
riscriviamo un blank, rimaniamo in q0 e ci spostiamo a
destra. Ed è proprio quello che dovremo fare per scorrere
il nastro fino al primo "1". Sempre da tabella, vediamo cosa
succede quando incontriamo un "1" dallo stato q0. Leggiamo
b-q1-D: vuol dire che scriviamo un blank (questa volta al
posto dell'"1") trasliamo nello stato q1 (inizia la seconda
fase, di cancellamento) e ci spostiamo a destra. In tale
stato, sempre come da tabella, continuiamo a scambiare "1"
con blank fino a quando non troviamo in lettura un blank
(abbiamo finito gli "1"). Nella tabella, in posizione stato
q1 - simbolo b, troviamo scritto "stop!", ciò che la
macchina in tale condizione, farà.
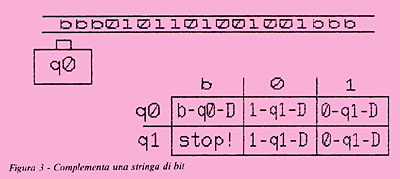 Secondo esempio: complemento a 1 di una stringa di bit
(figura 3).
La situazione
è analoga a quella precedente:
abbiamo una sequenza di caratteri diversi dal bank, immersa
nella miriade di blank di cui il nastro è composto.
Complemento ad 1 significa che dovremo sostituire ad ogni
"0" un "1" e viceversa. Sempre in figura 3
è mostrata la
corrispondente tabella che descrive il programma
"complemento". Stato iniziale e prima casella della tabella,
come prima: continuiamo a scorrere il nastro finché non
troviamo qualcosa diverso da un blank. A questo punto, se
troviamo uno "0" scriviamo un "1", trasliamo nello stato q1
e ci spostiamo a destra; se troviamo un "1" facciamo in
maniera analoga. Nello stato q1 procediamo a scambiare "0"
con "1" e viceversa (tenete sott'occhio sempre la tabella di
figura 3) fino a quando non troviamo un blank: abbiamo
finito e la macchina di Turing si può fermare.
Secondo esempio: complemento a 1 di una stringa di bit
(figura 3).
La situazione
è analoga a quella precedente:
abbiamo una sequenza di caratteri diversi dal bank, immersa
nella miriade di blank di cui il nastro è composto.
Complemento ad 1 significa che dovremo sostituire ad ogni
"0" un "1" e viceversa. Sempre in figura 3
è mostrata la
corrispondente tabella che descrive il programma
"complemento". Stato iniziale e prima casella della tabella,
come prima: continuiamo a scorrere il nastro finché non
troviamo qualcosa diverso da un blank. A questo punto, se
troviamo uno "0" scriviamo un "1", trasliamo nello stato q1
e ci spostiamo a destra; se troviamo un "1" facciamo in
maniera analoga. Nello stato q1 procediamo a scambiare "0"
con "1" e viceversa (tenete sott'occhio sempre la tabella di
figura 3) fino a quando non troviamo un blank: abbiamo
finito e la macchina di Turing si può fermare.
Terzo esempio (un tantino più complicato): decremento di un
numero binario di n bit, modulo 2^n (figura 4). Ovvero
preso un numero binario, si restituisce lo stesso numero
decrementato di uno, e se il numero di partenza era 0,
restituiamo il massimo numero binario rappresentabile con n
bit. Esattamente come accade
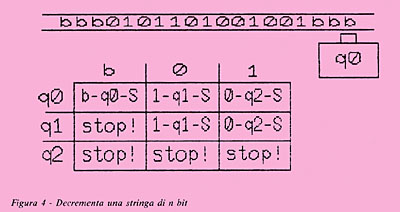 in linguaggio macchina e con un
qualsiasi registro del processore. In questo esempio, a
differenza di prima, la testina della macchina di Turing è
posizionata sui blank a destra del nostro numero binario,
quindi la prima cosa che farà sarà di scorrere verso
sinistra fino al primo simbolo non blank: vedasi prima
casella della tabella di figura 4 in cui con lettura di
blank e stato interno q0 (quello iniziale) si riscrive il
blank, si rimane in q0 e ci si sposta a sinistra.
in linguaggio macchina e con un
qualsiasi registro del processore. In questo esempio, a
differenza di prima, la testina della macchina di Turing è
posizionata sui blank a destra del nostro numero binario,
quindi la prima cosa che farà sarà di scorrere verso
sinistra fino al primo simbolo non blank: vedasi prima
casella della tabella di figura 4 in cui con lettura di
blank e stato interno q0 (quello iniziale) si riscrive il
blank, si rimane in q0 e ci si sposta a sinistra.
Se come primo carattere incontrato troviamo un "1",
è
sufficiente scrivere al suo posto uno "0" e abbiamo finito;
se incontriamo uno "0" bisogna ricorrere al ben noto
prestito delle scuole elementari ovvero scrivere un "1" e
manipolare le cifre successive tenendo conto che abbiamo un
debito. Ciò si traduce nel fatto che continueremo a
cambiare tutti gli "0" che incotreremo a sinistra con "1"
sino al prossimo "1" sul nastro che complementeremo per poi
fermare l'elaborazione. Se non troviamo altre cifre, ma un
blank, ci fermeremo ugualmente. Quanto qui descritto a
parole è esattamente ciò che è codificato nella tabella
in figura 4: lo stato q0 è quello iniziale, lo stato q1
quello in condizione di debito, lo stato q2 di stop.
 Infine, in figura 5, una macchina di Turing che, preso un
numero naturale, restituisce lo stesso moltiplicato per due.
Come nel caso precedente la scansione avviene da destra
verso sinistra (a tal proposito nella tabella inserita in
fig.5 per ragioni di spazio è stato omesso lo spostamento
della testina, da ritenersi sempre uguale a S, sinistra) e
la tentazione di lasciare al lettore l'arduo compito di raccapezzarsici,
è forte. Per aiuto comunque diremo che lo
stato q0 è come sempre quello iniziale, lo stato q1 è lo
stato in qui va la macchina quando raddoppia una cifra
minore di 5 (non c'è stato riporto), lo stato q2 è di
contro quello in cui si trova la macchina quando deve
riportare una unità (nel senso "elementare" del termine)
alla cifra successiva.
Infine, in figura 5, una macchina di Turing che, preso un
numero naturale, restituisce lo stesso moltiplicato per due.
Come nel caso precedente la scansione avviene da destra
verso sinistra (a tal proposito nella tabella inserita in
fig.5 per ragioni di spazio è stato omesso lo spostamento
della testina, da ritenersi sempre uguale a S, sinistra) e
la tentazione di lasciare al lettore l'arduo compito di raccapezzarsici,
è forte. Per aiuto comunque diremo che lo
stato q0 è come sempre quello iniziale, lo stato q1 è lo
stato in qui va la macchina quando raddoppia una cifra
minore di 5 (non c'è stato riporto), lo stato q2 è di
contro quello in cui si trova la macchina quando deve
riportare una unità (nel senso "elementare" del termine)
alla cifra successiva.
La tesi di Church
Dopo tutto questo parlare, è d'obbligo una domanda: siamo
proprio sicuri che la Macchina di Turing sia in grado di
calcolare qualsiasi funzione calcolabile? O meglio: esiste
una dimostrazione del fatto che qualsiasi altro formalismo
prendiamo esso non è più potente dell'automa di Turing?
Una tale dimostrazione non esiste: secondo Church e la sua
tesi, qualunque algoritmo prendiamo, scritto in qualsiasi
formalismo, esso può essere calcolato da una apposita MDT.
Lo stesso affermò che tale macchina non solo esiste, ma è
possibile costruirla effettivamente partendo dall'algoritmo e
dal formalismo in questione. Purtroppo Church morì prima di
riuscire a dimostrare il suo asserto e oggi, quello che
poteva essere il teorema più importante della teoria della
computabilità resta solo una tesi. Ovviamente ci potrà
riuscire qualcun altro così come potrebbe essere dimostrato
che Church aveva torto.
Resta però da sottolineare il fatto che altri formalismi,
completamente diversi da quello di Turing, partoriti in
epoche assai diverse e per vie diverse, messi a confronto,
risultano essere meno potenti o avere la stessa
potenzialità della MDT. Il confronto consiste naturalmente
nel fornire un procedimento effettivo (ed eseguibile) per
passare da un formalismo ad un altro. Quando riusciamo a
passare indifferentemente dal primo al secondo e viceversa,
i due formalismi sono equipotenti, se ci si riesce solo in
un verso è più potente quello che, ovviamente, riesce a
coprire anche gli algoritmi calcolati dall'altro. In tutte
le ricerche effettuate e a confronti avvenuti, semplicemente
il formalismo della macchina di Turing non è stato mai
"battuto".
Tutto qui.




 Velocità
di esecuzione a parte (nella teoria della calcolabilità non
contano certo i tempi d'esecuzione ma esclusivamente IL
FATTO se una determinata "cosa" sia calcolabile o meno) per
quanto possa sembrare strano, ripeto, qualsiasi programma
"eseguito" è una funzione matematica da N in N (i computer
trattano in ingresso e in uscita comunque solo ed
esclusivamente numeri), e in quanto tale può essere
calcolata dalla Macchina di Turing.
Velocità
di esecuzione a parte (nella teoria della calcolabilità non
contano certo i tempi d'esecuzione ma esclusivamente IL
FATTO se una determinata "cosa" sia calcolabile o meno) per
quanto possa sembrare strano, ripeto, qualsiasi programma
"eseguito" è una funzione matematica da N in N (i computer
trattano in ingresso e in uscita comunque solo ed
esclusivamente numeri), e in quanto tale può essere
calcolata dalla Macchina di Turing.  di un oggetto capace di calcolare. Se
però
dimentichiamo per un attimo la memoria, la MDT diventa un
oggetto, non solo tangibile, ma realizzabile con pezzi
elettromeccanici di fortuna come dei ricambi di un
registratore a bobina e una manciata di componenti allo
stato solido di vario genere. Infatti, una MDT è composta
essenzialmente da tre parti: un nastro magnetico, una
testina di registrazione/riproduzione e una parte di
controllo (figura 1).
di un oggetto capace di calcolare. Se
però
dimentichiamo per un attimo la memoria, la MDT diventa un
oggetto, non solo tangibile, ma realizzabile con pezzi
elettromeccanici di fortuna come dei ricambi di un
registratore a bobina e una manciata di componenti allo
stato solido di vario genere. Infatti, una MDT è composta
essenzialmente da tre parti: un nastro magnetico, una
testina di registrazione/riproduzione e una parte di
controllo (figura 1). 
 Secondo esempio: complemento a 1 di una stringa di bit
(figura 3).
La situazione
è analoga a quella precedente:
abbiamo una sequenza di caratteri diversi dal bank, immersa
nella miriade di blank di cui il nastro è composto.
Complemento ad 1 significa che dovremo sostituire ad ogni
"0" un "1" e viceversa. Sempre in figura 3
è mostrata la
corrispondente tabella che descrive il programma
"complemento". Stato iniziale e prima casella della tabella,
come prima: continuiamo a scorrere il nastro finché non
troviamo qualcosa diverso da un blank. A questo punto, se
troviamo uno "0" scriviamo un "1", trasliamo nello stato q1
e ci spostiamo a destra; se troviamo un "1" facciamo in
maniera analoga. Nello stato q1 procediamo a scambiare "0"
con "1" e viceversa (tenete sott'occhio sempre la tabella di
figura 3) fino a quando non troviamo un blank: abbiamo
finito e la macchina di Turing si può fermare.
Secondo esempio: complemento a 1 di una stringa di bit
(figura 3).
La situazione
è analoga a quella precedente:
abbiamo una sequenza di caratteri diversi dal bank, immersa
nella miriade di blank di cui il nastro è composto.
Complemento ad 1 significa che dovremo sostituire ad ogni
"0" un "1" e viceversa. Sempre in figura 3
è mostrata la
corrispondente tabella che descrive il programma
"complemento". Stato iniziale e prima casella della tabella,
come prima: continuiamo a scorrere il nastro finché non
troviamo qualcosa diverso da un blank. A questo punto, se
troviamo uno "0" scriviamo un "1", trasliamo nello stato q1
e ci spostiamo a destra; se troviamo un "1" facciamo in
maniera analoga. Nello stato q1 procediamo a scambiare "0"
con "1" e viceversa (tenete sott'occhio sempre la tabella di
figura 3) fino a quando non troviamo un blank: abbiamo
finito e la macchina di Turing si può fermare. in linguaggio macchina e con un
qualsiasi registro del processore. In questo esempio, a
differenza di prima, la testina della macchina di Turing è
posizionata sui blank a destra del nostro numero binario,
quindi la prima cosa che farà sarà di scorrere verso
sinistra fino al primo simbolo non blank: vedasi prima
casella della tabella di figura 4 in cui con lettura di
blank e stato interno q0 (quello iniziale) si riscrive il
blank, si rimane in q0 e ci si sposta a sinistra.
in linguaggio macchina e con un
qualsiasi registro del processore. In questo esempio, a
differenza di prima, la testina della macchina di Turing è
posizionata sui blank a destra del nostro numero binario,
quindi la prima cosa che farà sarà di scorrere verso
sinistra fino al primo simbolo non blank: vedasi prima
casella della tabella di figura 4 in cui con lettura di
blank e stato interno q0 (quello iniziale) si riscrive il
blank, si rimane in q0 e ci si sposta a sinistra. Infine, in figura 5, una macchina di Turing che, preso un
numero naturale, restituisce lo stesso moltiplicato per due.
Come nel caso precedente la scansione avviene da destra
verso sinistra (a tal proposito nella tabella inserita in
fig.5 per ragioni di spazio è stato omesso lo spostamento
della testina, da ritenersi sempre uguale a S, sinistra) e
la tentazione di lasciare al lettore l'arduo compito di raccapezzarsici,
è forte. Per aiuto comunque diremo che lo
stato q0 è come sempre quello iniziale, lo stato q1 è lo
stato in qui va la macchina quando raddoppia una cifra
minore di 5 (non c'è stato riporto), lo stato q2 è di
contro quello in cui si trova la macchina quando deve
riportare una unità (nel senso "elementare" del termine)
alla cifra successiva.
Infine, in figura 5, una macchina di Turing che, preso un
numero naturale, restituisce lo stesso moltiplicato per due.
Come nel caso precedente la scansione avviene da destra
verso sinistra (a tal proposito nella tabella inserita in
fig.5 per ragioni di spazio è stato omesso lo spostamento
della testina, da ritenersi sempre uguale a S, sinistra) e
la tentazione di lasciare al lettore l'arduo compito di raccapezzarsici,
è forte. Per aiuto comunque diremo che lo
stato q0 è come sempre quello iniziale, lo stato q1 è lo
stato in qui va la macchina quando raddoppia una cifra
minore di 5 (non c'è stato riporto), lo stato q2 è di
contro quello in cui si trova la macchina quando deve
riportare una unità (nel senso "elementare" del termine)
alla cifra successiva.